Реферат: Похідні та диференціали функції багатьох змінних
Реферат: Похідні та диференціали функції багатьох змінних
ПОХІДНІ ТА ДИФЕРЕНЦІАЛИ
ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ
1 Частинні
похідні
Нехай функція 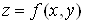 визначена в
деякому околі точки визначена в
деякому околі точки 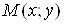 . .
Надамо змінній x приросту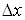 , залишаючи
змінну , залишаючи
змінну 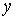 незмінною,
так, щоб точка незмінною,
так, щоб точка 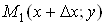 належала заданому околу. належала заданому околу.
Величина
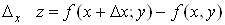
називається
частинним приростом функції 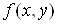 за змінною x. за змінною x.
Аналогічно
вводиться частинний приріст 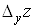 функції за змінною функції за змінною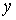 : :
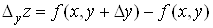 . .
Якщо існує
границя
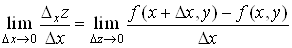 , ,
то вона
називається частинною похідною функції 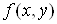 в точці в точці 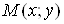 за змінною x і позначається одним
із таких символів: за змінною x і позначається одним
із таких символів:
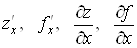 . .
Аналогічно
частинна похідна функції 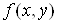 за за 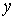 визначається як границя визначається як границя
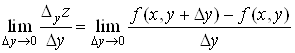
і позначається
одним із символів:
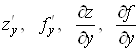 . .
Згідно з
означенням при знаходженні частинної похідної 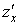 обчислюють звичайну похідну
функції однієї змінної x, вважаючи змінну обчислюють звичайну похідну
функції однієї змінної x, вважаючи змінну  сталою, а при знаходженні
похідної сталою, а при знаходженні
похідної  сталою
вважається змінна x. Тому частинні похідні знаходять за формулами і правилами
обчислення похідних функцій однієї змінної. сталою
вважається змінна x. Тому частинні похідні знаходять за формулами і правилами
обчислення похідних функцій однієї змінної.
Частинна похідна 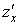 (або (або ) характеризує
швидкість зміни функції в напрямі осі ) характеризує
швидкість зміни функції в напрямі осі 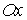 (або (або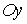 ). ).
З’ясуємо
геометричний зміст частинних похідних функції двох змінних. Графіком функції 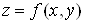 є деяка
поверхня (рис 1). Графіком функції є деяка
поверхня (рис 1). Графіком функції 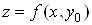 є лінія перетину цієї поверхні з
площиною є лінія перетину цієї поверхні з
площиною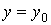 .
Виходячи з геометричного змісту похідної для функції однієї змінної, отримаємо,
що .
Виходячи з геометричного змісту похідної для функції однієї змінної, отримаємо,
що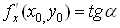 , де , де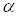 – кут між віссю – кут між віссю
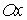 і
дотичною, проведеною до кривої і
дотичною, проведеною до кривої 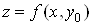 в точці в точці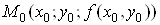 . Аналогічно . Аналогічно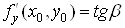 . .
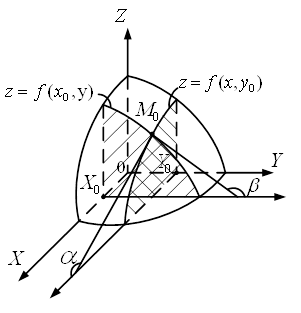
Рисунок 1 –
Геометричний зміст частинних похідних
Для функції 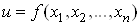 n змінних
можна знайти n частинних похідних: n змінних
можна знайти n частинних похідних:
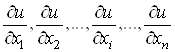 , ,
де
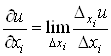 , ,
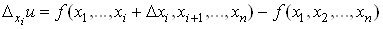 . .
Щоб знайти
частинну похідну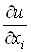 , необхідно взяти звичайну похідну
функції , необхідно взяти звичайну похідну
функції 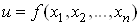 за
змінною за
змінною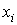 , вважаючи
решту змінних сталими. , вважаючи
решту змінних сталими.
Якщо функція 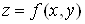 задана в
області задана в
області 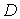 і
має частинні похідні і
має частинні похідні 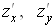 в усіх точках в усіх точках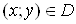 , то ці похідні можна
розглядати як нові функції, задані в області , то ці похідні можна
розглядати як нові функції, задані в області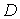 . .
Якщо існує
частинна похідна за x від функції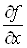 , то її називають частинною
похідною другого порядку від функції , то її називають частинною
похідною другого порядку від функції 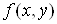 за змінною x і позначають за змінною x і позначають 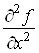 або або 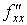 . .
Таким чином, за
означенням
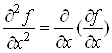 або або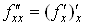 . .
Якщо існує
частинна похідна від функції 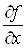 за змінною за змінною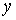 , то цю похідну
називають мішаною частинною похідною другого порядку від функції , то цю похідну
називають мішаною частинною похідною другого порядку від функції 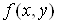 і позначають і позначають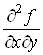 , або , або . .
Отже, за означенням
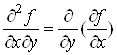 або або 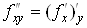 . .
Для функції двох
змінних 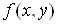 можна
розглядати чотири похідні другого порядку: можна
розглядати чотири похідні другого порядку:
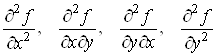 . .
Якщо існують
частинні похідні від частинних похідних другого порядку, то їх називають
частинними похідними третього порядку функції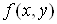 , їх вісім: , їх вісім:
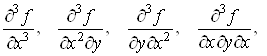
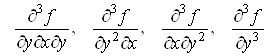 . .
Виникає
запитання: чи залежить результат диференціювання від порядку диференціювання?
Інакше кажучи, чи будуть рівними між собою мішані похідні, якщо вони взяті за
одними і тими самими змінними, одне й те саме число разів, але в різному
порядку? Наприклад, чи дорівнюють одна одній похідні
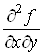 і і 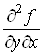 або або 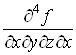 і і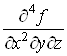 ? ?
У загальному
випадку відповідь на це запитання негативна.
Проте справедлива
теорема, яку вперше довів К.Г.Шварц.
Теорема (про мішані похідні). Якщо
функція 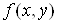 визначена
разом із своїми похідними визначена
разом із своїми похідними 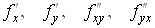 в деякому околі точки в деякому околі точки 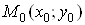 , причому
похідні , причому
похідні  та та
 неперервні
в точці неперервні
в точці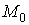 ,
то в цій точці ,
то в цій точці
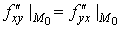 . .
Аналогічна
теорема справедлива для будь-яких неперервних мішаних похідних, які
відрізняються між собою лише порядком диференціювання.
2 Диференційованість
функції
похідна
диференціал функція змінна
Нехай функція 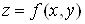 визначена в
деякому околі точки визначена в
деякому околі точки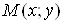 . Виберемо прирости . Виберемо прирости 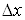 і і 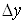 так, щоб точка так, щоб точка 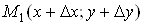 належала
розглядуваному околу і знайдемо повний приріст функції в точці належала
розглядуваному околу і знайдемо повний приріст функції в точці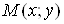 : :
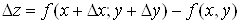 . .
Функція 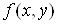 називається
диференційовною в точці М, якщо її повний приріст в цій точці можна подати у
вигляді називається
диференційовною в точці М, якщо її повний приріст в цій точці можна подати у
вигляді
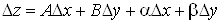 , (1) , (1)
де 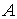 та та 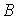 – дійсні числа, які не
залежать від – дійсні числа, які не
залежать від 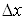 та та 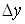 , ,  – нескінченно малі при – нескінченно малі при 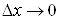 і і 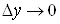 функції. функції.
Відомо, що коли
функція однієї змінної диференційовна в деякій точці, то вона в цій точці
неперервна і має похідну. Перенесемо ці властивості на функції двох змінних.
Теорема 1 (неперервність
диференційовної функції).
Якщо функція 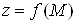 диференційовна
в точці М, то вона неперервна в цій точці. диференційовна
в точці М, то вона неперервна в цій точці.
Доведення
Якщо функція
диференційовна в точці М, то з рівності (1) випливає, що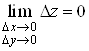 . Це означає, що функція
неперервна в точці М. . Це означає, що функція
неперервна в точці М.
Теорема 2 (існування частинних похідних
диференційовної функції). Якщо функція 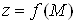 диференційовна в точці диференційовна в точці 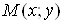 , то вона має в
цій точці похідні , то вона має в
цій точці похідні 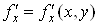 та та 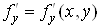 і і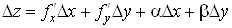 . .
Доведення
Оскільки 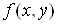 диференційовна
в точці диференційовна
в точці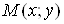 ,
то справджується рівність (1). Поклавши в ній ,
то справджується рівність (1). Поклавши в ній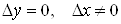 , отримаємо, , отримаємо,
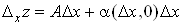 . .
Поділимо обидві
частини цієї рівності на 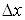 і перейдемо до границі при і перейдемо до границі при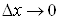 : :
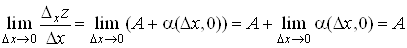 . .
Отже, в точці 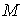 існує частинна
похідна існує частинна
похідна .
Аналогічно доводиться, що в точці .
Аналогічно доводиться, що в точці 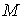 існує частинна похідна існує частинна похідна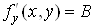 . .
Твердження,
обернені до теорем 1 і 2, взагалі кажучи, неправильні, тобто із неперервності
функції 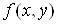 або
існування її частинних похідних ще не випливає диференційовність. Наприклад,
функція або
існування її частинних похідних ще не випливає диференційовність. Наприклад,
функція 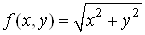 неперервна
в точці неперервна
в точці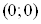 ,
але не диференційовна в цій точці. Справді, границі ,
але не диференційовна в цій точці. Справді, границі

не існує, тому не
існує й похідної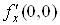 . Аналогічно впевнюємося, що не
існує також похідної . Аналогічно впевнюємося, що не
існує також похідної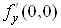 . Оскільки задана функція в точці . Оскільки задана функція в точці 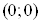 не має частинних
похідних, то вона в цій точці не диференційовна. не має частинних
похідних, то вона в цій точці не диференційовна.
Більш того,
відомо приклади функцій, які є неперервними в деяких точках і мають в них
частинні похідні, але не є в цих точках диференційовними.
Теорема 3 (достатні умови
диференційовності ).
Якщо функція 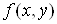 має частинні
похідні в деякому околі точки має частинні
похідні в деякому околі точки 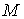 і ці похідні неперервні в точці М,
то функція і ці похідні неперервні в точці М,
то функція 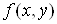 диференційовна
в точці М. диференційовна
в точці М.
Доведення
Надамо змінним x
і 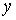 приростів приростів
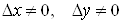 , таких,
щоб точка , таких,
щоб точка 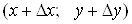 належала
даному околу точки належала
даному околу точки 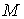 . Повний приріст функції . Повний приріст функції 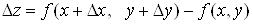 запишемо у
вигляді запишемо у
вигляді
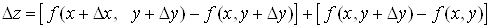 . (2) . (2)
Вираз у перших
квадратних дужках рівності (2) можна розглядати як приріст функції однієї
змінної x, а в других – як приріст функції змінної 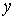 . Оскільки дана функція має
частинні похідні, то за теоремою Лагранжа отримаємо: . Оскільки дана функція має
частинні похідні, то за теоремою Лагранжа отримаємо:
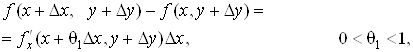
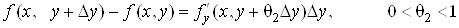 . .
Похідні 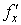 та та  неперервні в
точці М, тому неперервні в
точці М, тому
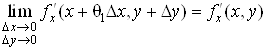 , ,
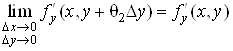 . .
Звідси випливає,
що
 , ,
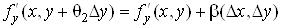 , ,
де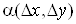 , , 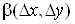 – нескінченно малі
функції при – нескінченно малі
функції при 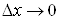 і і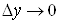 . .
Підставляючи ці
вирази у рівність (2), знаходимо
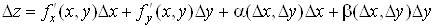 , а це й означає, що функція , а це й означає, що функція
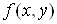 диференційовна
в точці диференційовна
в точці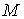 . .
З теорем 2 і 3
випливає такий наслідок: щоб функція 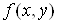 була диференційовною в точці,
необхідно, щоб вона мала в цій точці частинні похідні, і достатньо, щоб вона
мала в цій точці неперервні частинні похідні. була диференційовною в точці,
необхідно, щоб вона мала в цій точці частинні похідні, і достатньо, щоб вона
мала в цій точці неперервні частинні похідні.
Зазначимо, що для
функції 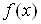 однієї
змінної існування похідної однієї
змінної існування похідної 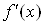 в точці в точці 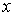 є необхідною і достатньою умовою
її диференційовності в цій точці. є необхідною і достатньою умовою
її диференційовності в цій точці.
3 Повний
диференціал функції та його застосування до обчислення функцій і похибок.
Диференціали вищих порядків
Нагадаємо, що
коли функція 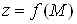 диференційовна в точці диференційовна в точці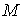 , то її повний
приріст у цій точці можна подати у вигляді , то її повний
приріст у цій точці можна подати у вигляді
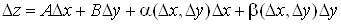 , ,
де 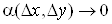 і і 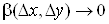 при при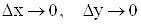 . .
Повним
диференціалом 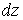 диференційовної в точці диференційовної в точці 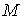 функції функції 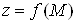 називається
лінійна відносно називається
лінійна відносно 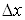 та та 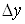 частина повного приросту цієї
функції в точці M, тобто частина повного приросту цієї
функції в точці M, тобто
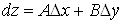 . (3) . (3)
Диференціалами
незалежних змінних x та 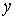 назвемо прирости цих змінних назвемо прирости цих змінних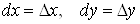 . Тоді з
урахуванням теореми 2 рівність (3) можна записати так: . Тоді з
урахуванням теореми 2 рівність (3) можна записати так:
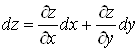 . (4) . (4)
Аналогічна
формула має місце для диференційовної функції трьох змінних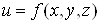 : :
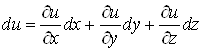 . (5) . (5)
З формул (4) і
(5) може здатися, що повний диференціал 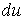 існуватиме у кожній точці, в якій
існують частинні похідні. Але це не так. Згідно з означенням, повний
диференціал можна розглядати лише стосовно диференційовної функції. існуватиме у кожній точці, в якій
існують частинні похідні. Але це не так. Згідно з означенням, повний
диференціал можна розглядати лише стосовно диференційовної функції.
Теореми та
формули для диференціалів функції однієї змінної повністю зберігаються і для
диференціалів функцій двох, трьох і т.д. змінних . Так, незалежно від того, від
яких аргументів залежать функції u і 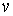 , завжди справедливі рівності , завжди справедливі рівності
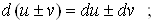
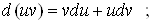
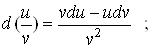

Покажемо, що
різниця між повним приростом 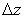 і диференціалом і диференціалом 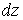 при при  і і 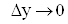 є нескінченно мала
величина вищого порядку, ніж величина є нескінченно мала
величина вищого порядку, ніж величина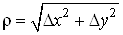 . .
Дійсно, з формул
(1) і (3) маємо
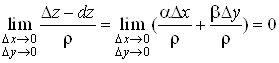 , ,
оскільки функції 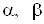 – нескінченно
малі при – нескінченно
малі при , , 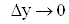 , а , а 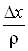 та та 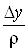 – обмежені
функції: – обмежені
функції:
 . .
Отже, різниця 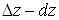 – нескінченно
мала величина вищого порядку, ніж – нескінченно
мала величина вищого порядку, ніж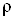 . Тому повний диференціал
називають також головною частиною повного приросту диференційовної функції. При
цьому виконується наближена рівність . Тому повний диференціал
називають також головною частиною повного приросту диференційовної функції. При
цьому виконується наближена рівність 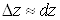 або або
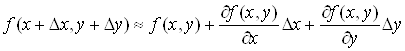 . (6) . (6)
Ця рівність тим
точніша, чим менша величина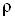 . Рівність (6) широко
використовується у наближених обчисленнях, оскільки диференціал функції
обчислюється простіше, ніж повний приріст. . Рівність (6) широко
використовується у наближених обчисленнях, оскільки диференціал функції
обчислюється простіше, ніж повний приріст.
Покажемо, як за
допомогою диференціала можна оцінити похибку в обчисленнях.
Нехай задана
диференційовна функція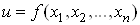 , незалежні змінні якої виміряні з
точністю , незалежні змінні якої виміряні з
точністю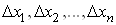 .
Потрібно знайти похибку, з якою обчислюється u. .
Потрібно знайти похибку, з якою обчислюється u.
Природно вважати,
що ця похибка дорівнює величині
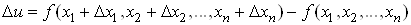 . .
Для малих значень
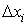 маємо маємо
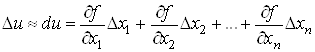 , ,
звідки
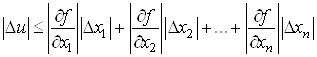 . .
Якщо через 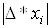 позначити
максимальну абсолютну похибку змінної позначити
максимальну абсолютну похибку змінної 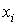 , то можна отримати значення
максимальної абсолютної похибки , то можна отримати значення
максимальної абсолютної похибки 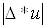 функції функції 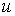 : :
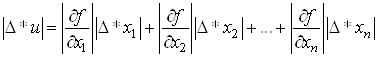 . (7) . (7)
Щоб оцінити
максимальну відносну похибку функції u, поділимо обидві частини рівності (7) на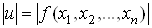 : :
 . .
Оскільки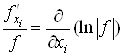 , то , то
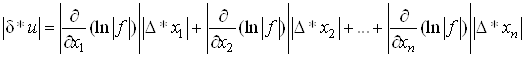 , ,
або
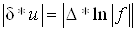 , ,
тобто максимальна
відносна похибка функції дорівнює максимальній абсолютній похибці її логарифма.
Введемо поняття
диференціала вищого порядку.
Нехай 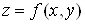 функція
незалежних змінних функція
незалежних змінних 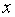 , ,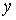 . Повний диференціал цієї функції,
знайдений за формулою (3), називають ще диференціалом . Повний диференціал цієї функції,
знайдений за формулою (3), називають ще диференціалом
першого порядку. Диференціал другого порядку визначають за формулою
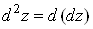 . .
Тоді, якщо
функція 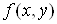 має
неперервні частинні похідні, то має
неперервні частинні похідні, то
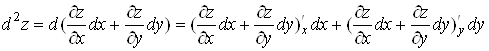 , ,
звідки
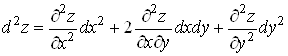 . (8) . (8)
Символічно це
записують так:
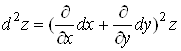 . .
Аналогічно можна
отримати формулу для диференціала третього порядку:
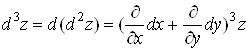 . .
Застосовуючи
метод математичної індукції, можна отримати формулу для диференціала n-го
порядку:
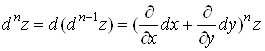 . (9) . (9)
Зазначимо, що
формула (9) справедлива лише для випадку, коли змінні x і 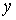 функції функції 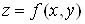 є незалежними змінними. є незалежними змінними.
4 Похідна
складеної функції. Повна похідна. Інваріантність форми повного диференціала
Нехай 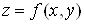 – функція двох
змінних – функція двох
змінних 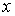 та та
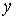 , кожна з
яких, у свою чергу, є функцією незалежної змінної , кожна з
яких, у свою чергу, є функцією незалежної змінної 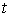 : :
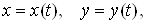
тоді функція 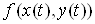 є складеною
функцією змінної є складеною
функцією змінної 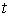 . .
Теорема. Якщо функції 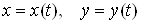 диференційовні в точці диференційовні в точці 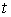 , а функція , а функція 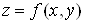 диференційовна в точці диференційовна в точці 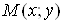 , то складена функція , то складена функція 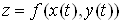 також
диференційовна в точці також
диференційовна в точці 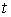 . Похідну цієї
функції знаходять за формулою . Похідну цієї
функції знаходять за формулою
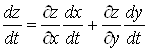 . (10) . (10)
Доведення
За умовою теореми
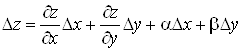 , ,
де  та та  при при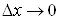 , ,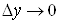 . .
Поділимо 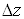 на на  і перейдемо до
границі при і перейдемо до
границі при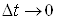 : :

Аналогічно
знаходять похідну, якщо число проміжних змінних більше двох. Наприклад, якщо 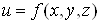 , де , де 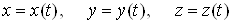 , то , то
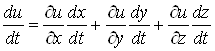 . (11) . (11)
Зокрема, якщо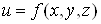 , а , а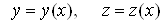 , то , то
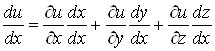 , ,
а оскільки  , то , то
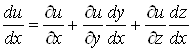 . (12) . (12)
Цю формулу
називають формулою для обчислення повної похідної
(на відміну від частинної похідної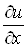 ). ).
Розглянемо
загальніший випадок. Нехай 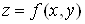 – функція двох змінних – функція двох змінних 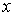 та та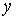 , які, в свою
чергу, залежать від змінних , які, в свою
чергу, залежать від змінних 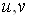 : :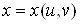 , , 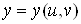 , тоді функція , тоді функція 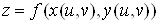 є складеною функцією
незалежних змінних є складеною функцією
незалежних змінних 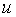 та та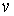 , а змінні , а змінні 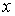 та та 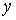 – проміжні. – проміжні.
Аналогічно
попередній теоремі доводиться таке твердження.
Якщо функції 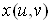 та та 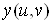 диференційовні
в точці диференційовні
в точці 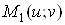 ,
а функція ,
а функція 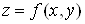 диференційовна
в точці диференційовна
в точці 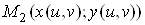 ,
то складена функція ,
то складена функція 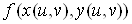 диференційовна в точці диференційовна в точці 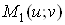 і її частинні
похідні знаходяться за формулами: і її частинні
похідні знаходяться за формулами:
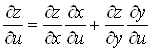 ; ; 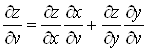 . (13) . (13)
Формули (13)
можна узагальнити на випадок більшого числа змінних. Якщо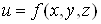 , де , де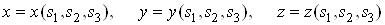 , то , то
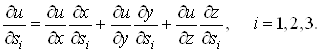
Знайдемо
диференціал складеної функції. Скориставшись формулами (13), отримаємо
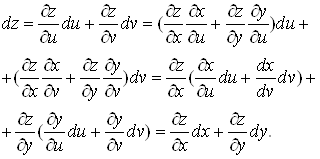
Отже, диференціал
функції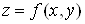 ,
де ,
де 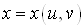 , , 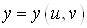 , визначається
формулою , визначається
формулою
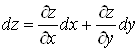 ,
(14) ,
(14)
де
 . .
Порівнявши
формули (14) і (4) дійдемо висновку, що повний диференціал функції 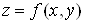 має
інваріантну (незмінну) форму незалежно від того, чи є x та має
інваріантну (незмінну) форму незалежно від того, чи є x та 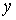 незалежними змінними,
чи диференційовними функціями змінних u та v. Проте формули (4) і (14) однакові
лише за формою, а по суті різні, бо у формулі (4) незалежними змінними,
чи диференційовними функціями змінних u та v. Проте формули (4) і (14) однакові
лише за формою, а по суті різні, бо у формулі (4) 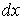 і і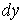 – диференціали незалежних змінних,
а у формулі (14) – диференціали незалежних змінних,
а у формулі (14) 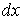 і і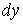 – повні диференціали функцій – повні диференціали функцій 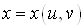 та та 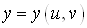 . .
Диференціали
вищих порядків властивості інваріантності не мають. Наприклад, якщо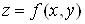 , де , де 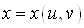 , , 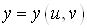 , то , то
 (15) (15)
Формула (15)
відрізняється від формули (8), оскільки для складеної функції диференціали 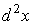 та та 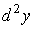 можуть і не
дорівнювати нулю. Отже, для складеної функції можуть і не
дорівнювати нулю. Отже, для складеної функції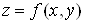 , де , де 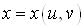 , , 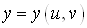 , формула (8) неправильна. , формула (8) неправильна.
5
Диференціювання неявної функції
Нехай задано
рівняння
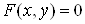 , (16) , (16)
де 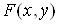 – функція двох змінних. – функція двох змінних.
Нагадаємо, що
коли кожному значенню x з деякої множини 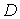 відповідає єдине значення відповідає єдине значення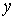 , яке разом з x
задовольняє рівняння (16), то кажуть, що це рівняння задає на множині , яке разом з x
задовольняє рівняння (16), то кажуть, що це рівняння задає на множині 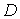 неявну функцію неявну функцію . .
Таким чином, для
неявної функції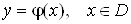 , заданої рівнянням (16), має
місце тотожність , заданої рівнянням (16), має
місце тотожність
 . .
Які ж умови має
задовольняти функція 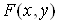 щоб рівняння (16) визначало
неявну функцію і при тому єдину? Відповідь на це запитання дає така теорема
існування неявної функції [8]. щоб рівняння (16) визначало
неявну функцію і при тому єдину? Відповідь на це запитання дає така теорема
існування неявної функції [8].
Теорема. Нехай функція 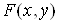 і її похідні і її похідні 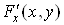 та та 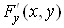 визначені та
неперервні у будь-якому околі точки визначені та
неперервні у будь-якому околі точки 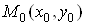 і і  , а , а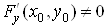 ; тоді існує окіл точки ; тоді існує окіл точки 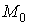 , в якому
рівняння , в якому
рівняння 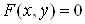 визначає
єдину неявну функцію визначає
єдину неявну функцію , неперервну та диференційовну в
околі точки , неперервну та диференційовну в
околі точки 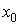 і
таку, що і
таку, що 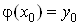 . .
Знайдемо похідну
неявної функції. Нехай ліва частина рівняння (16) задовольняє зазначені в
теоремі умови, тоді це рівняння задає неявну функцію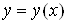 , для якої на деякій множині точок
x має місце тотожність , для якої на деякій множині точок
x має місце тотожність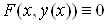 . Оскільки похідна функції, що
тотожно дорівнює нулю, також дорівнює нулю, то повна похідна . Оскільки похідна функції, що
тотожно дорівнює нулю, також дорівнює нулю, то повна похідна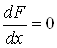 . Але за формулою (12)
маємо . Але за формулою (12)
маємо 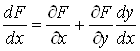 ,
тому ,
тому 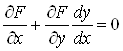 ,
звідки ,
звідки
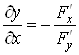 .
(17) .
(17)
За цією формулою
знаходять похідну неявної функції однієї змінної.
|





