Реферат: Привод электродвигателя

= 1,1;

 – коэффициент, учитывающий влияние деформационного упрочнения или электрохимической обработки переходной поверхности. Для зубьев колес без деформационного упрочнения или электрохимической обработки переходной поверхности зубьев принимают

= 1;

 – коэффициент, учитывающий влияние двухстороннего приложения нагрузки. При одностороннем приложении нагрузки

= 1;

 – коэффициент долговечности. Для длительно работающих передач принимается

= 1;

Учитывая все найденные коэффициенты определим :

  – коэффициент безопасности, который равен

                                                                                                              Таблица 3

  – коэффициент, учитывающий градиент напряжения и чувствительность материала к концентрации напряжений. При проектном расчете открытых зубчатых передач принимаем

  – коэффициент, учитывающий шероховатость переходной поверхности. Для шлифования и зубофрезерования при шероховатости не ниже RZ40 принимают = 1. при полировании  в зависимости от способа термического упрочнения принимают: при цементации, нитроцементации, азотировании = 1,05; при нормализации и улучшении = 1,2.

= 1,2;

 – коэффициент, учитывающий размеры зубчатого колеса. Определяют в зависимости от диаметра вершин зубчатого колеса по специальному графику [1].

= 1.

Определив все величины и коэффициенты, входящие в формулу, находим :

Определяем ориентировочное значение модуля m:

Полученное значение округляем до стандартного в соответствии c ГОСТ 9563–60 [1]:

3.  Определяем диаметры начальных (внешних) делительных окружностей шестерни и колеса.

Диаметр начальной делительной окружности шестерни:

Диаметр начальной делительной окружности колеса:

4.  Определяем межосевое расстояние.

5.  Определяем окружную скорость.

где ω1 – угловая скорость на валу шестерни, с-1,

6.  Определяем степень точности передачи.

 Степень точности выбирают  в зависимости от назначения передачи, условий ее работы и возможности производства. Открытые цилиндрические зубчатые передачи обычно выполняют по 9-ой степени точности.

7.  Определяем рабочую ширину венца шестерни и колеса.

8.  Проведем проверочный расчет зубьев на выносливость при изгибе

Расчетное напряжение изгиба зубьев  определяют по формуле

где  – удельная расчетная окружная сила.

Для цилиндрических прямозубых передач

где  – крутящий момент на валу шестерни, который берется из таблицы 1:

  – коэффициент, учитывающий распределение нагрузки между зубьями. Расчет зубчатых колес первоначально производят, предполагая, что в зацеплении находится одна пара зубьев. Тогда

= 1;

  – коэффициент, учитывающий распределение нагрузки по ширине венца. См. п. 2.

  – коэффициент, учитывающий динамическую нагрузку, возникшую в зацеплении:

= 1;

  – коэффициент, учитывающий форму зуба. См. п. 2.

= 4,05;

  – коэффициент, учитывающий перекрытие зубьев:

= 1;

  – коэффициент, учитывающий наклон зуба:

= 1;

Определив все величины и коэффициенты, входящие в формулу, находим напряжение изгиба зубьев:

Найденное значение напряжения изгиба зубьев соответствует условиям расчета.

 4.  Расчет закрытой передачи (цилиндрического редуктора)

4.1. Выбор материала зубчатой передачи

В проектируемых редукторах рекомендуется применять термически обработанные среднеуглеродистые не легированные стали 45, 40Х.

Сталь в настоящее время — основной материал для изготовления зубчатых колес. В условиях индивидуального и мелкосерийного производства применяют зубчатые колеса с твердостью материала не превосходящей 350 НВ. При этом обеспечивается чистовое нарезание зубьев после термообработки, высокая точность изготовления и хорошая прирабатываемость зубьев.

Определяем марку стали: для шестерни – 40Х, твердость ≥ 45HRCэ1; для колеса 40Х, твердость ≤350 НВ2 [1, с.49]. Разность средних твердостей          НВ1ср – НВ2ср ≥ 70.

Определяем механические характеристики стали 40Х: для шестерни твер-дость 269...302 НВ1, термообработка – улучшение и закалка ТВЧ. Определяем среднюю твердость зубьев шестерни и колеса:

                      НВ1ср = 285,5

                      НВ2ср = (235 + 262)/2 = 248,5.                                   

4.2. Определение допускаемых контактных напряжений [σ]Н

Допускаемые контактные напряжения при расчетах на прочность определяются отдельно для зубьев шестерни [σ]Н1 и колеса [σ]Н2.

Рассчитываем коэффициент долговечности КHL. Наработка за весь срок службы:

для колеса:          N2 = 573ω2Lh,                  

                              N1=48,26∙107 циклов;

для шестерни:     N1 = N2∙uзп,                    

                              N2=10, 72∙107  циклов.

Число циклов перемены напряжений NН0, соответствующее пределу выносливости, находим по табл. 3.3 [3] интерполированием:

 NН01 = 25∙106 циклов;

 NН02 = 25∙106 циклов.

   Так как N1>NН01 и N2>NН02, то коэффициенты долговечности КНL1 = 1 и

КHL2 = 1.

   Так как N1>NН01 и N2>NН02, то коэффициенты долговечности КНL1 = 1 и КHL2 = 1.

Определяем допускаемое контактное напряжение [σ]Н0, соответствующее числу циклов перемены напряжений NН0     [3]

для шестерни:

                   [σ]Н01=1,8HВ1ср+67                                           

                   [σ]Н01= 1,8∙285,5+67=580,9  Н/мм2;

для колеса:

                   [σ]Н02=1,8HВ2ср+67                                               

                   [σ]Н02= 1,8∙248,5+67=514,3 Н/мм2.

Определяем допускаемое контактное напряжение:

для шестерни:

                               [σ]Н1=КHL1∙[σ]Н01                                                                                

                    [σ]Н1= 1∙580,9=580,9 Н/мм2;

для колеса:

            [σ]Н2=КHL2∙[σ]Н02                                                                                 

                    [σ]Н2= 1∙514,3=514,3 Н/мм2.

Так как НВ1ср – НВ2ср =285,5   – 248,5 = 20…50 НВ, то косозубая передача рассчитывается на прочность по меньшему допускаемому контактному напряжению.

4.3 Определение допускаемых напряжений изгиба [σ]F

Рассчитываем коэффициент долговечности КFL. Наработка за весь срок службы:

для колеса        N2 = 10,72∙107  циклов;

для шестерни     N1 =48,26∙107 циклов.

Число циклов перемены напряжений, соответствующее пределу выносливости, NF0 = 4∙106 для обоих колес.

Так как N1>NF01 и N2>NF02, то коэффициенты долговечности

КFL1 = 1 и КFL2 = 1.

Определяем допускаемое напряжение изгиба [3], соответствующее числу циклов перемены напряжений NF0:

для шестерни:

                      [σ]F01 = 294,07 Н/мм2 в предположении, что m<8 мм;                                    

для колеса:             

                      [σ]F02 = 1,03HВ2ср = 1,03∙248,5 =255,96 Н/мм2.                          

Определяем допускаемое напряжение изгиба:

для шестерни:

                      [σ]F1 =294,07  Н/мм2;                                  

для колеса:

                      [σ]F2 =255,96 Н/мм2.                                  

Таблица 4

Составляем табличный ответ к задаче:

4.4 Проектный расчет закрытой зубчатой передачи

        1. Определяем главный параметр — межосевое расстояние аW, мм:

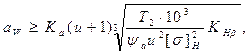
где  Ка — вспомогательный коэффициент. Для косозубых передач Ка = 43;

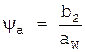        - коэффициент ширины венца колеса, равный 0,28...0,36 - для шестерни, расположенной симметрично относительно опор в проектируемых нестандартных одноступенчатых цилиндрических редукторах. Примем его равным 0,30;

       u - передаточное число редуктора;

       Т2 - вращающий момент на тихоходом валу редуктора, Н/м;

      [s]Н - допускаемое контактное напряжение колеса с ме­нее прочным зубом или среднее допускаемое контактное напряжение, Н/мм2;

      КНb - коэффициент неравномерности нагрузки по длине зуба. Для прирабатывающихся зубьев КНb = 1.

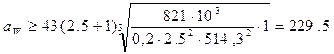                                                                                                                                              (мм)              

aw=230 мм

         2. Определяем модуль зацепления m, мм:

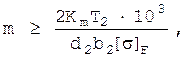
где  Кm — вспомогательный коэффициент. Для косозубых передач Кm = 5,8;

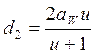        - делительный  диаметр колеса, мм, d2=271,5 мм;

        b2 = yaaW  - ширина венца колеса, мм, b2= 48 мм;

       [s]F —среднее допускаемое контактное напряжение , Н/мм2.

Таким образом, m = 2.16, округляя до стандартного значения, принимаем                              m=2,5(мм).

        3. Определяем угол наклона зубьев bmin для косозубых передач:

                                                       ,

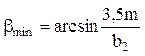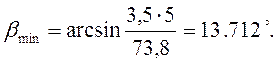
       4. Определяем суммарное число зубьев шестерни и колеса для косозубых колес:

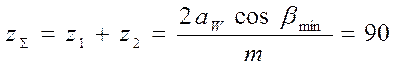
        5.Уточняем действительную величину угла наклона зубьев для косозубых передач:

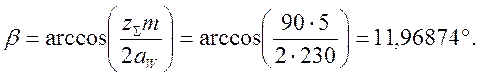
        6.Определяем число зубьев шестерни:

                                   .

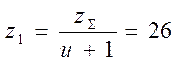      7. Определяем число зубьев колеса:

                              z2 = zΣ – z1 =90 - 26=64                             .

       8. Определяем фактическое передаточное число uф:

                                                                           .

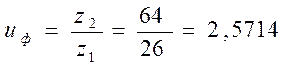и проверяем его отклонение от заданного:

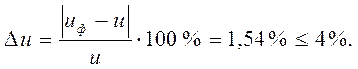
      9. Определяем фактическое межосевое расстояние для косозубых передач:

               .

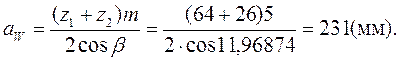Геометрические параметры пере­дачи представлены в табл. 5.

Таблица 5

Геометрические параметры пере­дачи

.4.5. Проверочный расчет

1. Проверяем межосевое расстояние:

                                 .

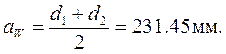2.Проверяем контактные напряжения sН:

                  .

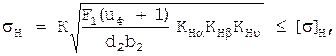где К - вспомогательный коэффициент. Для косозубых передач К = 376;

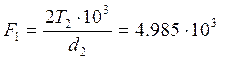
— окружная сила в зацеплении, Н;

КНa - коэффициент, учитывающий распределение нагрузки между зубьями. Зависит от окружной скорости колес 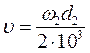, и степени точности передачи, принимаем равной 8; КНa=1,119 [1, с.62-63];

КНu — коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи, КНu=1,01 [1, с.62].

Подставляя числовые данные получаем:

3.Проверяем напряжения изгиба зубьев шестерни sF1 и колеса sF2, Н/мм2:

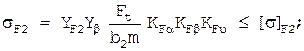
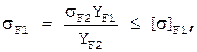
где  m - модуль зацепления, мм;

        b2 - ширина зубчатого венца колеса, мм;

        Ft - окружная сила в зацеплении, Н;

KFa - коэффициент, учитывающий распределение нагрузки между зубьями. Для косозубых колес КFa зависит от степени точности передачи. КFa = 1,0.

КFb — коэффициент неравномерности нагрузки по длине зуба. Для прирабатывающихся зубьев колес КFb = 1;

КFu — коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи равный 1,04, [3];

YF1 и YF2 — коэффициенты формы зуба шестерни и колеса. Для косозубых определяются в зависимости от эквивалентного числа зубьев шестерни

                                                                            .

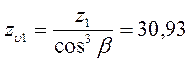 и колеса

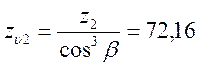                                                  YF1 = 3,88    и   YF2 = 3,62;

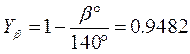 — коэффициент, учитывающий наклон зуба;

[s]F1 и [s]F2 — допускаемые напряжения изгиба шестерни и колеса, Н/мм2.

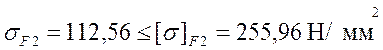
Составляем табличный ответ*, мм:

                                                                                                                       Таблица 6

 Проверочный расчет

4.6. Определение сил в зацеплении

                                                                                           Таблица 7        Значения сил

Страницы: 1, 2, 3